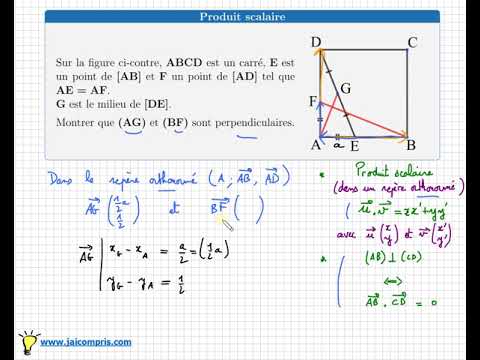
|
EN BREF
|
Dans le domaine de la géométrie, il est essentiel de comprendre comment établir que deux droites sont parallèles. Cette notion est fondamentale, car deux droites parallèles ne se croisent jamais, quel que soit leur prolongement. Plusieurs méthodes permettent d’effectuer cette démonstration. Parmi celles-ci, la comparaison des angles formés par une sécante ou l’utilisation des propriétés des vecteurs sont des approches courantes. En maîtrisant ces techniques, il devient plus facile d’analyser des figures géométriques et de résoudre des problèmes liés à la disposition des droites dans l’espace.
La question de la parallélisme des droites est un concept central en géométrie. Cet article explore différentes méthodes pour déterminer si deux droites sont parallèles. Nous aborderons divers critères et propriétés géométriques qui peuvent être utilisés, comme les angles, les distances et le théorème de Thalès. Que vous soyez étudiant ou simplement intéressé par la géométrie, ces notions vous permettront de mieux appréhender ce sujet fascinant.
Critères de parallélisme basés sur les angles
Une des méthodes les plus courantes pour démontrer que deux droites sont parallèles repose sur l’analyse des angles qu’elles forment avec une droite sécante. Si deux droites coupées par une sécante déterminent des angles correspondants de même mesure, alors ces droites sont parallèles. Par exemple, si les angles A et B sont égaux lorsque la droite sécante traverse les deux droites, vous pouvez conclure que celles-ci sont parallèles.
Angles alternés
De plus, la propriété des angles alternés permet également d’établir le parallélisme. Si vous constatez que deux angles alternés formés par une sécante traversant deux droites sont égaux, cela signifie que les deux droites sont parallèles. La visualisation de cette situation à l’aide d’un schéma géométrique peut grandement aider à saisir cette notion.
Utilisation du théorème de Thalès
Le théorème de Thalès est un outil puissant pour prouver le parallélisme. Selon la réciproque du théorème, si deux droites sont coupées par une même sécante et qu’elles forment des segments proportionnels, alors elles sont parallèles. Pour appliquer ce théorème, il suffit de vérifier les longueurs des segments créés par la sécante sur les deux droites.
Propriétés des segments proportionnels
Pour illustrer cela, considérons trois points alignés sur une même droite. Si les longueurs des segments entre ces points respectent une proportionnalité, cela démontre que les droites sont parallèles. Une bonne technique consiste à tracer les segments et à les mesurer avec précision pour en vérifier les rapports.
Analyse des pentes
Une autre approche pour démontrer que deux droites sont parallèles consiste à examiner leurs pentes. Si vous disposez des équations des deux droites, vous pouvez calculer leurs pentes respectives. Deux droites sont parallèles si et seulement si leurs pentes sont égales. Cela peut être particulièrement utile dans le cadre des coordonnées cartésiennes.
Calcul des pentes
Pour calculer la pente d’une droite donnée par les points A(x1, y1) et B(x2, y2), on utilise la formule suivante : (y2 – y1) / (x2 – x1). En appliquant cette formule aux deux droites et en comparant les résultats, vous pourrez confirmer si elles sont parallèles ou non.
Approche avec les vecteurs
Enfin, une méthode plus avancée impliquerait l’utilisation de vecteurs. Deux droites peuvent être considérées comme parallèles si les vecteurs normaux qui leur sont associés sont colinéaires. Soit d et d’ deux droites ; si leurs vecteurs normaux sont multiples l’un de l’autre, alors les deux droites sont parallèles.
Colinéarité des vecteurs
Pour vérifier la colinéarité, il suffit d’étudier les coefficients des vecteurs. Si vous pouvez exprimer un vecteur en fonction d’un multiple d’un autre vecteur, cela prouve que les droites sont parallèles. Cette approche est souvent utilisée dans les études plus avancées de la géométrie analytique.
Comparaison des Méthodes pour Démontrer que des Droites sont Parallèles
| Méthode | Description |
| Angles Correspondants | Si deux droites coupées par une sécante forment des angles correspondants égaux, alors elles sont parallèles. |
| Angles Alternés Internes | Si deux droites sont coupées par une sécante et qu’elles forment des angles alternés internes égaux, elles sont parallèles. |
| Réciproque de Thalès | Si des segments de droites sont proportionnels, cela prouve que les droites sont parallèles. |
| Pentes Égales | Deux droites ayant la même pente dans le plan sont parallèles. |
| Vecteurs Normaux | Si les vecteurs normaux de deux droites sont colinéaires, alors les droites sont parallèles. |
Comprendre comment démontrer que des droites sont parallèles est essentiel en géométrie. Ce concept fondamental repose sur plusieurs critères et propriétés qui permettent de vérifier si deux droites ne se rencontreront jamais dans l’espace. Dans cet article, nous explorerons différentes méthodes pour établir ce lien entre les droites grâce à des angles, des théorèmes et des propriétés géométriques.
Utilisation des angles correspondants
Une méthode couramment utilisée pour démontrer que deux droites sont parallèles consiste à observer les angles correspondants. Si deux droites, lorsqu’elles sont coupées par une sécante, forment des angles correspondants de même mesure, alors ces droites sont nécessairement parallèles. Ce principe se base sur le fait que les angles qui se retrouvent dans une position correspondante, par rapport à la sécante, auront des valeurs identiques si les droites sont parallèles.
Théorème de Thalès
Le théorème de Thalès est une autre approche efficace. Selon ce théorème, si une transversale coupe deux droites en formant des segments proportionnels, alors les droites sont parallèles. La réciproque de ce théorème peut donc être utilisée pour prouver que les droites ne se croiseront jamais. En vérifiant les longueurs des segments formés, on peut ainsi établir la parallélisme entre ces droites.
Critère des pentes
Le critère des pentes est particulièrement utile lorsque les droites sont représentées par des équations. Deux droites sont parallèles si leurs pentes sont égales. On peut déterminer la pente d’une droite à partir de l’équation de celle-ci. Si les pentes des deux droites s’avèrent identiques, alors elles sont confirmées comme étant parallèles.
Colinéarité des vecteurs normaux
Enfin, une autre méthode pour démontrer que des droites sont parallèles implique l’analyse des vecteurs. Si les vecteurs normaux des droites sont colinéaires, cela signifie qu’ils partagent la même direction, ce qui indique que les droites elles-mêmes sont parallèles. Cette méthode est souvent utilisée dans le cadre de la géométrie analytique.
- Critère des angles correspondants : Si deux droites coupées par une sécante forment des angles correspondants de même mesure, alors elles sont parallèles.
- Critère des angles alternés : Si deux droites sont coupées par une sécante et que les angles alternés sont égaux, alors les droites sont parallèles.
- Critère des angles internes : Si deux droites sont coupées par une sécante et que les angles internes sur le même côté sont supplémentaires, alors les droites sont parallèles.
- Propriété des droites perpendiculaires : Si deux droites sont perpendiculaires à une même troisième droite, alors elles sont parallèles entre elles.
- Réciproque du théorème de Thalès : Si les points de deux droites sont alignés selon un même rapport, alors ces droites sont parallèles.
- Colinéarité des vecteurs normaux : Deux droites sont parallèles si les vecteurs normaux qui leur sont associés sont colinéaires.
- Critère des pentes : Si les pentes de deux droites sont égales, alors ces droites sont parallèles.
Dans l’étude de la géométrie, il est essentiel de pouvoir démontrer que certaines droites sont parallèles. Ce concept est fondamental car il a des implications dans de nombreux domaines des mathématiques et de la physique. Les méthodes pour établir la parallélisme des droites peuvent varier en fonction des informations disponibles. Cet article explique les différentes approches permettant de prouver que deux droites sont parallèles, en mettant l’accent sur l’utilisation d’angles et des théorèmes pertinents.
Utilisation des Angles Correspondants
Une des méthodes les plus simples pour démontrer que deux droites sont parallèles est celle des angles correspondants. Si deux droites sont coupées par une sécante et que les angles formés à chaque intersection sont de même mesure, alors ces deux droites sont parallèles. Cela repose sur la propriété suivante : lorsque des angles correspondants sont égaux, les droites qui les déterminent ne se croiseront jamais.
Exemple Pratique
Considérons deux droites, d et d’, coupées par une sécante. Si l’angle A formé par la droite d et la sécante est égal à l’angle B formé par la droite d’ et la même sécante, alors d et d’ sont parallèles. Pour visualiser cette situation, un schéma aide à voir la relation entre les angles et les droites.
Théorème de Thalès
Le théorème de Thalès est un autre outil puissant pour prouver que deux droites sont parallèles. La réciproque de ce théorème indique que si deux droites sont coupées par une sécante et que les segments déterminés sur ces droites sont proportionnels, alors les deux droites sont parallèles.
Application de la Réciproque de Thalès
Imaginons trois points alignés sur la première droite et trois autres points alignés sur la seconde, formant ainsi une sécante. Si les longueurs des segments formés sur les deux droites sont proportionnelles, nous pouvons conclure que les deux droites sont parallèles. Cette méthode est particulièrement utile dans le cadre de l’exercice avec des segments de longueur donnée.
Application des Vecteurs Normaux
Une autre méthode pour établir que deux droites sont parallèles passe par l’utilisation des vecteurs. Deux droites sont considérées comme parallèles si leurs vecteurs normaux sont colinéaires. Cela signifie qu’il existe un facteur de proportionnalité entre les directions des droites.
Méthode de Calcul
Pour démontrer cela, il suffit de déterminer les vecteurs directs des deux droites et de vérifier si l’un est un multiple de l’autre. Par exemple, si nous avons les équations de deux droites sous forme paramétrique ou vectorielle, nous pourrons facilement calculer et comparer les vecteurs associés.
Conclusion des Méthodes de Vérification
Pour prouver que deux droites sont parallèles, plusieurs méthodes peuvent être appliquées. Que ce soit par les angles correspondants, l’application du théorème de Thalès ou l’analyse des vecteurs normaux, chacune d’elles offre une approche claire et efficace. Choisir la méthode dépendra souvent du contexte et des données disponibles.